Gridding and Dimensionality

Although there is great value in directly visualizing measured data; it does have many limitations. Without mapping sparse measured data to a grid, computation of contaminant areas or volumes is not possible. Further, the techniques available for visualizing the data are very limited. For these reasons and more, significant attention should be paid to the process of creating a grid into which the data will be interpolated and extrapolated.

For this paper, a grid is defined as a collection of nodes and cells. Nodes are points in two or three-dimensions with coordinates and usually one or more data values. The word "cell" and "element" are both used as a generic term to refer to geometric objects. The cell type and the nodes that comprise their vertices define these objects. Commonly used cell types are described in Table 1.1 and Figure 1.8.

Cell Type	Number of Nodes	Dimensionality
Point	1	0
Line	2	1
Triangle	3	2
Quadrilateral	4	2
Tetrahedron	4	3
Pyramid	5	3
Prism	6	3
Hexahedron	8	3

Table 0.1 Common Cell Types

Dimensionality refers to the space occupied by the cell. Points have do not have length, width, or height, therefore their dimensionality is zero (0). Lines are dimensionality "1" because they have length. Dimensionality 2 objects such as quadrilaterals (quad) and triangles have area and dimensionality 3 objects ranging from tetrahedrons (tet) to hexahedrons (hex) are volumetric. When creating a two-dimensional grid, areal cells are used and for three-dimensional grids, volumetric cells are used.

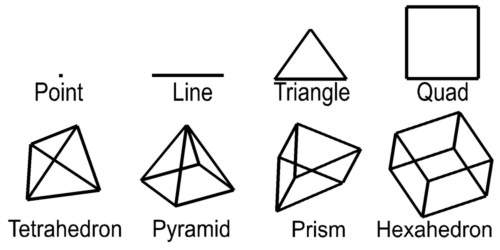
Figure0.7Common Cell Types